
Spirituality & The Brain (Home Page)
What caused the Big Bang?
Todd Murphy, (updated 2022) Contact Us by Email.
The prevalence of rotation in the universe, and some recent evidence makes the postulate that the collapsed universe was rotating prior to the Big Bang appear reasonable. Even though the mass of the universe may have been collapsed to a singularity, so that it’s rotation becomes difficult to conceptualize, there is still the rotation of its gravitational field to be considered.
The rotation of gravitational fields has been termed “inertial dragging” and has been explored by physicists J.M. Cohen and D.R. Brill. The following equation gives the angular speed of rotation of inertial frames. at a distance R from the center of a rotating mass of angular velocity J Where Ω is inertial dragging, G is the gravitational constant, and c is the velocity of light in vacuo.
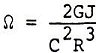
According to Newton’s law for centrifugal force, a body in circular orbit around a mass M at a distance R from the center will have a linear escape velocity when:
V2 = GM/R (V2 = velocity squared), will have an escape velocity equal to the speed of light when:
M/R = C2/2g (C2 = square of the speed of light), since the square of the escape speed is twice the square of the circular orbit speed.
This implies that R=2GM/C2 (C2 = square of the speed of light).*
I offer the suggestion that high-velocity special relativistic effects operating, not on the collapsed universe’s mass, but rather on its gravitational field, might ‘stop’ gravitation when the field’s inertial dragging reaches the angular equivalent of the velocity of light.
At the velocity of light, time stops, and matter collapses into radiation. If gravitation were to demonstrate similar effects, the range of phenomena that might appear when the rotation of its gravitational field reached the angular equivalent of the velocity of light might include a ‘cancellation’ of gravitational effects, just as temporal effects stop at its linear velocity. Release of the potential energy bound in the hyper-compressed mass of the universe might account for its expansion.
In another scenario, should the angular velocity for inertial dragging exceed that of light, then the possibility appears that the collapsed mass of the universe might be affected by gravitation (as well as space/time) in the opposite (outward) direction, just as time goes backward for a mass with a velocity greater than the speed of light.
The effect would be to radiate the mass of the universe outward in all directions, at tangents to positions on the event horizon at the time the radiation took place.
Both scenarios (rotation of the gravitational field at the velocity of light, and exceeding that value) posit expressions of Special Relativistic electrodynamics in a General Relativistic context, and require mathematical models outside the scope of this brief communication.
In either model, the mass of the universe would tend to move outward on tangents to the escape horizon. The bulk of the universe’s mass would tend to be attracted to itself, following long elliptical orbits around its center of gravity, unlike the strictly radial expansion implied in Hubble’s classical cosmology and Gamow’s oft-repeated illustrations of an expanding balloon. Indeed, there is recent evidence that the universe is rotating.
Such a distribution for the universe’s mass would make an open-ended expansion very unlikely. Assuming inertial dragging in the collapsed universe tends to support the conclusion that we live in an oscillating universe.
End.
References:
1) Cohen & Brill “Rotating Masses and Their Effect on Inertial Frames” http://journals.aps.org/pr/abstract/10.1103/ PhysRev.143.1011 Physics Review Letters, 25 March 1966
2) Cohen, J.M. & Brill, D.R. “Further examples of ‘machian’ effects of rotating bodies in general relativity“ Il Nuovo Cimento August 1968, Volume 56, Issue 2, pp 209-219 (1968) 56: 209. doi:10.1007/BF02710148
*Acknowledgment: The calculations were done by Carey C. Briggs (formerly of the Harvard-Smithsonian Center for Theoretical Astrophysics), applying the author’s parameters.
NEURAL STIMULATION: HUMAN EVOLUTION: SPIRITUAL OFF-SITE PAGES (OPEN IN NEW WINDOWS). NEAR-DEATH EXPERIENCES: BRAIN STUFF: OTHER STUFF:
![]()
Other Pages On This Site:
The God Helmet | Shiva Psychic Technology
Shakti – Magnetic Brain Stimulation
Inventing Shakti
Stimulating My Brain As A Spiritual Path
![]()
Origins of spirituality in Human Evolution
Role of Mystics and mysticism in Human Evolution.
The Gay Male Brain in human evolution
The Evolution of Human Belief in God
Consciousness | Darwinian Reincarnation
![]()
NEUROSCIENCEArticles on neurotheology, (or – spirituality and religion meet brain science).
Enlightenment And the Brain
Deja Vu | Meditations from Brain Science
Romantic Love and the Brain
The Sensed Presence | God in the Brain
Spiritual Aptitude Test | Sacred Lands
The Spiritual Personality | Archetypes
Out-Of-Body Experiences | Visions
Odd Experiences – Online Poll Results
Podcasts on Neurotheology
![]()
Different spiritual practices have different effects on the brain.
![]()
NDEs in Thailand – Discussion | Thai NDE Case histories
Darwinian Reincarnation
Near-Death Experience Screensaver (Entering the Light).
Epilepsy And Near-Death Experiences
![]()
Glasses For Enhanced Visual Acuity
A Diet For Epileptics?
Sex & States of Consciousness
Hippocrates on Epilepsy
The Terrorist Brain
![]()
Real-Time Geomagnetic levels
Credentials
What Caused The Big Bang?
PRIVACY POLICY